分布定数回路理解のための電子工学

　いきなり分布定数回路の話をせず、その基礎事項から始める。

１－１ 電子工学と電磁気学(物理学)の関係
１－２　直流 (Direct Current, DC)
１－３　オームの法則
１－４　交流 (Alternating Current, AC)
１－５　コンデンサ (Condenser, Capacitor)
１－６　コイル (Coil, Inductor)
１－７　インピーダンス

１－１　電子工学と電磁気学(物理学)の関係

　電気・電子工学(回路理論)は電磁気学を電気・電子分野に応用した学問である。

　基になる電磁気学の内容は

• クーロン力
• 静電場
• 導体と静電場 コンデンサー
• 定常電流 、オームの法則
• 電流と静磁場 ビオサバール、アンペールの法則
• 電磁誘導 コイル
• マクスウェルの方程式と電磁波
• 物質中の電磁場
• 変動する電磁場と物質

等である。これを基礎に電気・電子工学は構成されてゐる。電磁気学は波動の物理学の一部も含んでゐる。

　電気・電子工学は電磁気学を一定の条件で近似化した議論を展開する。それは多くの状況で近似化された電気・電子工学の説明で間に合ふからである。

「回路の理論は電磁気学を母体として、その一部を単純化した理想化をすることによつて得られる抽象的な理論体系である。」

　例へば、電流は電源の正極から負極へ流れるとしてゐるが、実態は負の電荷を持つ電子が負極から正極に移動することである。他には、波動の伝達時間を0と仮定して議論する場合もある。
　電気信号は現実には有限の速さを持ち、遠方には遅れて伝はる。これを無視することは近似である。つまり伝達の遅延時間を無視しても実用上充分な精度で議論ができるものに近似を適用するわけである。

　一方、近似が成り立たないものは、近似する前の一般的な原則に戻り考へる必要がある。

１－２　直流 (Direct Current, DC)

　時間的に向きが変化しない電流のこと。

　直流電圧とは時間的に向き(極性)が変化しない電圧のことをいふ。
但し狭義では極性に加へ時間的に大きさも変化しない電圧のことをいふ。
　　例／安定化電源、短時間での電池電圧
　　狭義の直流(電流)とは時間的に向きも大きさも変化しない電流のことをいふ。
　　狭義では、極性は変化しないが大きさが時間的に変化する電流を脈流といふ。

　電流が流れるとは、正電荷が電源の正極(+)から負極(-)に流れることとする。
　ここで電源の負荷として性質が変化しないものを取り付けると仮定する。電源電圧が一定ならば、電流も一定。電流は負極に向つて一定に流れ続ける。電流は電源から電源に一周して戻る。

　電流は記号　I　で表し単位は　A(アンペア)。導体断面を通過する電荷の1秒当りの移動量と定義される。電気量　Q ( C、クーロン)、時間t(秒)として
　I = Q / t (A)

１－３　オームの法則

　1826年にバイエルンの物理学者オーム (Georg Simon Ohm)によつて行はれた実験を記念して名付けられた。

１－３－１　電圧と電流の関係

　抵抗が一定であれば電流の大きさは電圧に比例し、また電圧が一定であれば電流の大きさは抵抗に反比例する。抵抗を大きくすると電流が小さくなるから、抵抗は電流の流れにくさを表す量である。
　抵抗 (Resistance)は、正式には「電気抵抗」といひ単位はオーム(Ω)が使はれる。

１－３－２　オームの法則

　ここで電流をI(A)、電圧をV(V)、抵抗をR(Ω)とすれば
　I = V / R 　　　式1-3-1

となる。これを変形して
　V = R I (V), R = V / I (Ω)

ともいへる。

　ここで式1-3-1を変形し、I = G V と表すとき G = 1 / R の関係が成り立つ。Gはコンダクタンス (Conductance)と呼び、単位はS(ジーメンス, Siemens)が使はれる。電流の流れやすさを示す量である。

V = R I の形は電圧を求めるときに都合がよい
I = G V の形は電流を求めるときに都合がよい

１－３－３　物質の電気抵抗

　物質の電気抵抗は、断面積が大きく、長さが短いほど小さい。電線でも太くて短いのが抵抗は小さい。
　一般に抵抗は長さと抵抗率に比例し、断面積に反比例する。
　抵抗率ρ(ロー)(Ωm)を持つ材料の長さを l (m)、断面積を S (㎡)とすれば、この材料の抵抗Rは、
R = ρ l / S (Ω)

で表される。

１－３－４　抵抗の直列接続

　複数の抵抗を一列に接続することを抵抗の直列接続といふ。

　3本の抵抗R1、R2、R3を直列に接続したときの全体の抵抗(合成抵抗)Rは
R = R1 + R2 + R3

１－３－５　抵抗の並列接続

　複数の抵抗の端をまとめて二点で接続することを抵抗の並列接続といふ。

　3本の抵抗R1、R2、R3を並列に接続したときの全体の抵抗(合成抵抗)Rは
　R = 1 / {(1 / R1) + (1 / R2) + (1 / R3)}

１－３－６　電力

　電気抵抗のある導体に電流を流すと熱が発生する。イギリスの物理学者ジュールの実験によつて、電流による単位時間当りの発熱量は電気抵抗と電流の2乗に比例することがわかつた。
　単位時間(1秒)当りの電気的エネルギーの消費を電力と呼び記号Pで表し、単位はワット(W)を使ふ。
抵抗をR、その両端の電圧をV、抵抗に流れる電流をIとすれば電力Pは、
P = I^2 R (W)

である。オームの法則によれば
P = V^2 / R とも P = V I

とも表せる。

１－４　交流 (Alternating Current, AC）

１－４－１　交流

　周期的に大きさと向きが変化する電流のこと。交番電流の略。
　直流電流は電源の正極から負極に流れる。しかし交流電源に正極、負極はない。電源コンセントに極性がない(基本的には)ことと同じである。
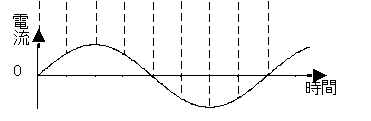
　交流の殆どは正弦波交流であるので、それについて話をする。

　上の図は正弦曲線である。正弦波交流はこの曲線に従つて変化する。横軸は角度である。0度から360度(2πラジアン)までが1周期。後は繰り返し。１秒間に繰り返す数を交流の周波数といひ、単位はHz(ヘルツ)である。
　狭義の直流の周波数は0Hzになる。

１－４－２　電流の変化

　交流の時間変化を追つてみる。

• 初期状態で電源電圧、電流が0であるとする。(図1-4-1)
• 電流は徐々に増えピークを迎へる。(図1-4-2、図1-4-3)
• そこから減少を始める。(図1-4-4)
• そして0になる。(図1-4-5)
• 今度は電流が逆方向に流れ始める。これは電源の極性が反転したことになる。(図1-4-6)
• 逆方向に電流は徐々に増えピークを迎へる。(図1-4-7)
• そこから減少を始める。(図1-4-8)
• そしてまた0に戻る。(図1-4-9)

これを繰り返す。
　電流0 の状態を中心にして電流の向きが引いては寄せる変化をする。これが正弦波交流の電流変化である。

図1-4-1	図1-4-2	図1-4-3
図1-4-4	図1-4-5	図1-4-6
図1-4-7	図1-4-8	図1-4-9

１－４－３　交流の電圧、電流

　交流の電圧は時間と共に変化する。では交流の電圧はどう表すのか。通常は実効値で表す。
　実効値とは、同じ電力を与へる直流電圧の値である。下図のやうに、交流電源に抵抗Rを接続する。直流電源に同じ値の抵抗Rをつなぎ同じ熱量を発生させるときの直流電圧Vが交流の実効値vになる。

　正弦波交流の実効値は最大値 (振幅、波高値、ピーク値ともいふ)の になる。最大値が141Vの正弦波交流の実効値は約100Vである。つまり日本の電源コンセントに来てゐる交流はこれであり、+141Vから-141Vまでの間を変化する。

　交流の電流も同様に実効値で表す。

１－４－４　正弦波の位相

　位相とは正弦曲線上の位置を示す言葉である。正弦曲線の値は角度で決る、つまり0度から360度まである。 　複数の正弦曲線の位置関係を表すのに位相差の表現を使ふ。

例

• 曲線ロは曲線イに対して位相が90度遅れてゐる。
• 曲線ロと曲線イの位相差は90度。

１－５　コンデンサ (Condenser, Capacitor)

１－５－１　静電誘導

　帯電した物質に他の金属を近付けると接近した部分には帯電物質とは異符号の電荷、遠い方には同符号の電荷が現れる。この現象を静電誘導といふ。

　正に帯電した帯電体(丸)が、金属(四角形)に接近すると金属内部の電荷が分れる。

１－５－２　静電容量

　2枚の金属板を向かひ合はせたものにスイッチと直流電源を図のやうに接続する。

スイッチを閉じて暫くしてからスイッチを開く。すると2枚の金属板に図のやうに電荷が蓄えられる。
　金属板の面積や間隔、金属板間の絶縁物(誘電体)の種類を変へると、電圧が一定であつても蓄えられる電荷の量が変化することが分つてゐる。
　このやうに電荷を蓄えることができる能力を静電容量といひ、記号Cで表し、単位にはF(ファラッド)を使ふ。
　金属板間の電圧V(V)、蓄えられる電荷Q(C、クーロン)との関係は、
　Q = C V (C)

　C = Q / V (F)

である。また電極の間隔と面積、誘電体との関係は次式で示される。
　C = 8.85 10^-12 εs S / d (F)

ここに電極の間隔を d、面積を S、誘電体の比誘電率を εs とした。

１－５－３　コンデンサの直列接続

　3本のコンデンサC1、C2、C3を直列に接続したときの合成静電容量Cは
　C = 1 / {(1 / C1) + (1 / C2) + (1 / C3)}

１－５－４　コンデンサの並列接続

　3本のコンデンサC1、C2、C3を並列に接続したときの合成静電容量Cは
　C = C1 + C2 + C3

１－５－４　コンデンサに電源をつなぐ

• コンデンサに直流電源をつなぐ

　コンデンサに直流電源をつなぐとその瞬間に電流が流れるが、コンデンサが満充電になると電流は止る。満充電とは、コンデンサの電圧が電源電圧に一致することをいふ。電源を接続すると電流はすぐに流れる一方で電圧は徐々に上がる
　下図は電源の出力端子でみた電圧変化である。電源電圧は V(V)、コンデンサには電荷がない状態とする。コンデンサを接続した瞬間電圧は 0V 迄下がるが、そこから徐々に上昇し電源電圧 V(V) に到達し変化が止る。

• コンデンサに交流電源をつなぐと交流が流れる。

　コンデンサの電極に充電された電荷が、交流電源の電圧低下に伴ひ放電され、電流の向きが反転する。電荷がなくなると逆極性に充電が始まり、交流電源の電圧上昇が始まると先程とは逆方向に放電が始まり、電流が反転する。下図は定常状態の電流と電圧の位相関係を示す。
　抵抗器に交流電源を接続した場合に比べると電流と電圧の変化が時間的にずれてゐるのが特徴である。

１－５－５　交流が流れるときの電圧と電流の比

　電流の定義から、一秒当りの移動する電気量が大きいと電流も大きい。また静電容量が大きいと電極に蓄へられる電気量も大きくなり一回当りの充放電の電気量も大きい。従つてコンデンサを流れる交流電流は次の関係を持つ。
　コンデンサを流れる交流電流 I は交流の周波数 f と静電容量 C に比例する。正確には
I = 2π f C V となり V = I / (2π f C)

つまりコンデンサの交流での電流の流れにくさは 1 / (2π f C) と表される。
　コンデンサ、コイルについては、交流に対する抵抗と同じ働きをリアクタンス(Reactance)と呼び X の記号で表す。単位はΩ(オーム)である。
　コンデンサのリアクタンスは Xc などと書かれる。
　一方電流の流れやすさコンダクタンスに対応するものをサセプタンス(Susceptance)と呼び B の記号で表し、単位は S(ジーメンス)である。
　まとめると Xc = 1 / (2π f C) 、Bc = 1 / Xc = 2π f C　である。

１－６　コイル (Coil, Inductor)

１－６－１　直流電流による磁場

　直流電流を流すと磁場が発生する。直流が作る磁場の向きは、導線を中心とする同心円の接線方向で、電流の方向に右ねじを進ませるときねじを回す向きに一致する。これを右ねじの法則といふ。

１－６－２　電磁誘導の法則

　変化する磁界の中に置かれたコイルに電流が流れる現象を電磁誘導といふ。誘導電流は電磁誘導によつてコイルの生じる起電力によるものであり、この起電力を誘導起電力といふ。
１． 誘導起電力は、誘導電流が作る磁場がコイルを貫く元の磁束の変化を妨げるやうな向きに生じる。(レンツの法則)
２． 誘導起電力はコイルを貫く磁束の変化する速さに比例する。(ファラデーの法則)

１－６－３　自己誘導と相互誘導

• 自己誘導

　コイルを流れる電流が変化するときにコイル自身に誘導起電力が生じる現象。
　コイルを貫く磁束 Φ はコイルを流れる電流Iに比例する。
　誘導起電力 Ve は電流の単位時間当りの変化に比例する。
Ve = -L ΔI / Δt (V)

　比例定数 L はコイルによつて決り、自己インダクタンスと呼ぶ。L の単位はヘンリー(H)で表す。
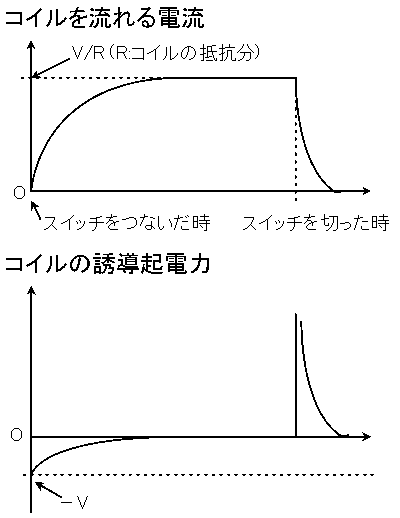
コイルによる誘導起電力Veは電流の変化を妨げる向きであることから逆起電力とも呼ぶ。

　スイッチを閉じた時点で誘導起電力は電源電圧と同じ値で発生し電流は徐々に増える。定常状態になつた後スイッチを開くと、今度は電流が急激に変化するため、コイルを貫く磁束にも大きな変化が生じ、それに伴ひ電源電圧よりも大きな起電力が発生する。

• 相互誘導

　下の右の図のやうに、二つのコイルを接近させておき、一次コイルによる磁束が二次コイルを貫くやうにしておくと、一次コイルの電流の変化によつて二次コイルを貫く磁束が変化し二次コイルに電圧が誘起される。これを相互誘導といふ。

１－６－４　コイルに電源をつなぐと

• 　直流についてはこれまで述べた通り。
• 　コイルに交流電源をつなぐと交流が流れる。

　電圧が反転すると電流が減少または増加し始める。それを繰り返す。 　コンデンサに比べると電流と電圧の変化が時間的に逆であるのが特徴。下図は定常状態の電流と電圧の位相関係を示す。

１－６－５　交流が流れるときの電圧と電流の比

　自己誘導現象から、電流の変化が速いと逆起電力が大きくなる。またインダクタンスが大きいと逆起電力が大きくなる。逆起電力が大きいことは電流が流れにくいことを意味する。従つてコイルを流れる交流電流は次の関係を持つ。
　コイルを流れる交流電流　I　は交流の周波数　f、インダクタンス　L　に反比例する。正確には
I = V / 2π f L となり V = 2π f L I

つまりコンデンサの交流での電流の流れにくさは 2π f L と表される。
　コイルのリアクタンスはXLなどと書かれる。

　まとめると XL = 2π f L 、BL = 1 / 2π f L　である。

１－７　インピーダンス

１－７－１　複素数で角度表現

　電気分野では虚数単位を i ではなく j で表す。理由は I や i が電流の記号であり紛らはしいため。
　念のため、電気分野では複素数を a + jb の形式で表記する。(数学と異なり a + bj とは書かない)
絶対値 |a + jb| = SQRT ( a^2 + b^2) である。

• 複素平面で角度を表す
  XY平面のX軸に実数、Y軸に虚数をとる。原点から指定された点を結ぶベクトルを考へる。

例
• 1 は長さ1、角度0度のベクトル
• j は長さ1、角度90度のベクトル
• -1 は長さ1、角度180度のベクトル
• -j は長さ1、角度-90度のベクトル
• 1/SQRT(2) + j / SQRT(2) は長さ1、角度45度のベクトル

• 掛け算は向きを変へる演算

j を掛けると+90度、j を2 回掛けると-1になり+180度、-j を掛けると-90度または+270度
　(∵ j^2 = -1, j^3 = j^2 * j = -j)

負の数を掛けることは180度向きを変へることを意味する。
90度進むのは j を掛ける。90度遅れるのは -j を掛ける。

１－７－２　インピーダンス (Impedance)

　コンデンサー、コイルによるリアクタンスと抵抗を統合し、交直両用にした抵抗の考へ方をインピーダンスといひ、記号Zで表す。

　抵抗、コイル、コンデンサが直列になつた回路を考へる。

全体のインピーダンスを Z、回路全体に掛かる電圧を V、回路に流れる電流を I とすれば
　V = Z I

Z は抵抗の直列接続と同様になり
　Z = R + j XL + (-j Xc) = R + j (XL - Xc)

V = Z I に上のZを代入し、括弧を展開すると
　V = {R + j (XL - Xc)} I = R I + j XL I - j Xc I

• コイルでは電流に対して電圧の位相が90度進んでゐる。→電流に j を掛けて電圧を計算する。
• コンデンサでは電流に対して電圧の位相が90度遅れてゐる。→電流に -j を掛けて電圧を計算する。

１－７－３　アドミタンス (Admittance)

　コンデンサー、コイルによるサセプタンスとコンダクタンスを統合し、交直両用にしたコンダクタンスの考へ方をアドミタンスといひ、記号Ｙで表す。
　Y = 1 / Z = G + j B = G + j (Bc - BL)　∴　I = {G + j (Bc - BL)} V = G V + j Bc V - j BL V　

　尚インピーダンスとアドミタンスを統合した概念をイミタンス(Immittance)といふ。

文献

• 岸源也「回路基礎論」コロナ社、S61年1月
• フリー百科事典Wikipedia「直流」「交流」の項
• 曽根他「図解　電気の大百科」オーム社、H8年9月
• 岡小天　他「高等学校物理」啓林館、昭和59年度用、第5章　電流と磁界