４－１　静電誘導
４－２　電磁誘導

４－１ 静電誘導

　１－５－１で簡単に述べた静電誘導について理解を深める。

４－１－１　静電誘導による導体の電位変化

　帯電した物体(帯電体)とグラウンドがあるとする。帯電体の電位はグラウンドを基準として 100V であるとする。帯電体とグラウンドの間に孤立した導体を置く(どこにも接続されてゐない導体)。するとこの導体の電位は帯電体とグラウンドとの距離に応じて 100V から 0V の間の値をとる。

　図では孤立導体を半分の距離に配置した。すると孤立導体の電位は 100V の半分の 50V になる。よく見るとこの状況はコンデンサの直列接続と同じことだと分る。孤立導体は二つのコンデンサの片側の電極とそれを結ぶ導線に相当する。帯電体直下のグラウンドには、帯電体の電荷と同量の負電荷が呼び集められてゐる。

　帯電体から孤立導体と孤立導体からグラウンドへの距離は同じなので、帯電体と孤立導体間の静電容量と孤立導体とグラウンド間の静電容量は同じになり、孤立導体で電圧は半分に分けられる。

　帯電体が孤立導体から遠ざかれば孤立導体の電位は下がる。近付くと電位は上がる。

• 　　　帯電体が遠ざかる―――＞孤立導体の電位が下がる
• 　　　帯電体が近付く　―――＞孤立導体の電位が上がる

　平行平板コンデンサの静電容量の式から、電極間の距離 d が大きくなると静電容量 C は小さくなり、距離 d が近くなると静電容量 C は大きくなる。

１－５－２「静電容量」

　帯電体の持つ電荷量Qは一定とすれば Q = C V の公式より、静電容量が小さくなればコンデンサの電極間の電圧 V は大きくなる。

　これを帯電体が遠ざかる話に当てはめると、帯電体と孤立導体間の静電容量Cが小さくなるので、帯電体と孤立導体間の電圧 V は 50V より大きくなる。(※帯電体の電位はどの場所でも変らない。常に 100V。) すると孤立導体とグラウンド間の電圧は、帯電体と孤立導体間が大きくなつた分 50V から小さくなる。

　要点は、孤立導体の電位は帯電体の距離によつて変化すること。
　また帯電体との距離が変らなくても、帯電体の電位が変化すると孤立導体の電位も同様に変化する。
　従つてプリント基板上に孤立導体があるのは好ましくない。普通はグラウンドに接続しておく。

４－１－２　静電誘導妨害

　完全に孤立してゐないがインピーダンスが高い信号線があるとする。そこに帯電体が接近してくると、その距離に応じて信号線の電位が変化する。

　線路のインピーダンスが高いことは、その単位長さ当りの静電容量が小さいことを意味する。
３－３「配線と静電場」

　逆に伝送線路のインピーダンスが低いことは、線路のグラウンドに対する静電容量が大きいことを意味する。コンデンサ2つが直列になつた左のモデルで考へる。 C1 が伝送線路のグラウンドに対する静電容量で、 C2 は線路と帯電体の間の静電容量である。通常、線路のすぐ側にグラウンドが存在する一方、帯電体は離れた場所にあるものだから C1 >> C2 となるであらう。

　帯電体による線路電圧の変化は、静電容量の比により決るから、帯電体の電圧の分配は C1 が小さく、 C2 が大きい。つまり C1 が大きいほど帯電体の影響を受けにくくなる。

４－１－３　静電遮蔽(静電シールド)

　導体によつて囲われた内部は外部電荷による静電誘導を受けない。これを静電遮蔽といふ。

　静電気の世界では一つの導体の電位はどこでも同じである。(分布常数回路の世界とは異なる。)空洞のある導体の内側から導体を見ると、どこも同じ電位であり、内部に電気力線が存在しない。電気力線は電位差のある所に存在するものである。
従つて外部電荷の存在は内部に影響しない。

(右の図はAgilent Technologies AppCADによる)

　同軸ケーブルは静電遮蔽されたケーブルである。内部導体は外部導体に完全に囲われてゐる。そのため内部導体は外部電荷の静電誘導を受けない。

　次に空洞のある導体の内部に正電荷が存在する場合を考へる。静電誘導により導体の内部は負電荷を帯び外側は正電荷を帯びる。従つて導体を外側から見ると正電荷を帯びてゐることになる。内部に電荷がある場合遮蔽されない。

　しかし遮蔽導体をグラウンドに接続すると、遮蔽導体外側にあつた正電荷はグラウンドに逃げ、空洞内部の電荷は外部に影響しなくなる。つまり囲ふ導体をグラウンドに接続すれば、その内側も外側の電荷の影響も他方に伝はらなくなる。

　これが信号線をグラウンド電位の導体で囲ふ理由である。信号線の変化も外部の変化も他方には伝はらず分離される。

４－２　電磁誘導

４－２－１　コイルにより発生する磁束

　コイルに発生する磁束 Φ はコイルに流れる電流 I に比例し、自己インダクタンスを L として

Φ = L I

の関係がある。コイルに流れる電流が変化すれば当然コイルから発生する磁束も変化する。

　自己インダクタンス L はコイルの巻き数と囲われる面積に比例して大きくなる。

図の1回巻きのコイル1とコイル2に同じ電流を流す場合には、コイル2がより多くの磁束を発生する。
因みにコイルの外側の磁束は0になる。磁束はコイルの内側に存在する。

４－２－２　電磁誘導ノイズ

　１－６－２「電磁誘導の法則」でも述べたやうに、コイル状の配線を貫く磁束が変化すると電磁誘導現象が発生する(レンツの法則)。

　電子回路のあるブロックの動作により磁束が変化すると、別のブロックにコイル状配線がある場合それに作用して誘導電圧が発生しノイズとなる。コイルの面積が大きいと影響を受ける、与へる範囲も広くなる。これは１－６－３で説明した相互誘導現象である。

　大きなコイルは磁束の放出量も大きく、誘導を受ける面積も大きくなる。

４－２－３　配線のL成分

　配線は微小な L (コイル)成分を持つ。

　図に示すやうに、電源と負荷を結ぶ回路そのものが1回巻きのコイルを形成してゐるからである。配線は一回巻きコイルの微少区間になり、小さなインダクタンスを持つ。分布定数回路の等価回路(３－２－１　分布定数回路)の L と考へて良い。

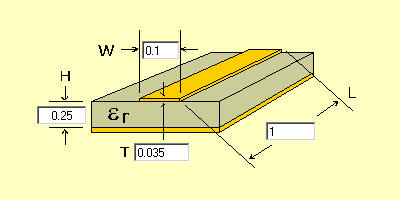
　下部にグラウンドを持ちマイクロストリップラインと見なせるプリント基板上の配線のインダクタンスは1mm当り0.1nHの桁である。値は機械的寸法により決り、基板の誘電率と原理的に無関係である。

　グラウンドとの距離が一定の時、配線が太ければ単位長さ当りのインダクタンスは減少する。

　以下の試算結果は、グラウンドと線路の距離を0.25mm、比誘電率を1.0、計算周波数を10MHzとしてSonnetにより試算した線路のリアクタンスから単位長さ当りの静電容量を求めた上、光速から計算した値である。

マイクロストリップライン1mm当りのインダクタンス(h=0.25mm)

配線幅(mm)	インダクタンス(nH/mm)
0.1	0.56
0.2	0.43
0.4	0.30
0.6	0.24
0.8	0.20
1.0	0.17

文献

• 伊藤健一「パスコンのはなし」日刊工業、2000年7月、23ページ
• 吉川浩「高速ディジタル伝送線路（１本）の場合の数学的基礎およびシミュレーション法」吉川浩氏のweb→実験室→「高速ディジタル伝送線路」の部屋の資料、2005年8月
• 有限会社ソネット技研「TEM線路の評価方法」ソネット技研web