２－１ キルヒホッフの法則
２－２　共振
２－３　コンデンサの周波数特性
２－４　コンデンサの使ひ方と反共振現象

２－１ キルヒホッフの法則

　抵抗や電池を組み合はせた複雑な回路では、オームの法則だけで各部分の電流を求めることは困難である。しかしキルヒホッフの法則を適用することで代数的に解くことができる。

２－１－１　キルヒホッフの電流法則(第一法則、Kirchhoff's Current Law, KCL)

　回路の分岐点に流れ込む電流を正、流れ出す電流を負とすれば、分岐点に流入する電流の総和は0になる。 　I1 + I2 + ... = 0 　式2-1-1

２－１－２　キルヒホッフの電圧法則(第二法則、Kirchhoff's Voltage Law, KVL)

　回路上の或る一回りの経路について、或る向きを正と決め、この向きに電流を流さうとする起電力およびこの向きに生じる電圧降下を正、逆の場合を負と決めると起電力の和は電圧降下の和に等しくなる。
　V1 + V2 + V3 ... = I1 R1 + I2 R2 + I2 R3 ... 　式2-1-2

２－２　共振

　特定の周波数でインピーダンス回路のリアクタンス分が0または無限大になることがある。これを共振といふ。

２－２－１　直列共振

　コイルL、コンデンサCが直列になつたインピーダンス回路を考へる。

この回路のインピーダンスを式で表すと、 　Z = j XL + (-j Xc) = j (XL - Xc) 　式2-2-1

　この回路は L と C のリアクタンス が等しいときにインピーダンスが 0 になる。この時、回路を流れる電流は最大になる。XL 、 Xc が等しくなる周波数を直列共振周波数といふ。
　回路のインピーダンスと周波数の関係をグラフで示すと次のやうになる。ω0 が直列共振周波数である。
　インピーダンスの虚数項が正の場合、合成リアクタンスはコイル (L) の性質を示す。これを誘導性、L性といふ。逆に虚数項が負の場合、合成リアクタンスはコンデンサ (C) の性質を示す。これを容量性、C性といふ。
　直列共振回路は共振周波数より低い周波数でリアクタンスは容量性となる。なぜなら Xc > XL であるから。高い周波数では Xc > XL であるため誘導性となる。

２－２－２　並列共振

　コイル L、コンデンサ C が並列になつたインピーダンス回路を考へる。

この回路のインピーダンスを式で表すと、
　Z = 1 / { 1 / (j XL) + 1 / (-j Xc) } = j (XL Xc) / (Xc - XL) 　式2-2-2

　この回路は L と C のリアクタンスが等しいときにインピーダンスが無限大になる。この時、回路の電圧は最大になる。L と C のリアクタンスが等しくなる周波数を並列共振周波数といふ。
　回路のインピーダンスと周波数の関係をグラフで示すと次のやうになる。並列共振周波数の下側では誘導性の無限大に、上側では容量性の無限大のリアクタンスになる。

２－２－３　共振周波数

　直列共振、並列共振ともにコンデンサとコイルのリアクタンスが一致した周波数であるから、
　Xc = XL 即ち　1 / (2π f C) = 2π f L

これから f (周波数)を求める。
　(2π f L) (2π f C) = (2π f)^2 L C = 1
　f^2 = 1 / {(2π)^2 L C} 従つて f = 1 / {2π * SQRT(L C)}　 式2-2-3

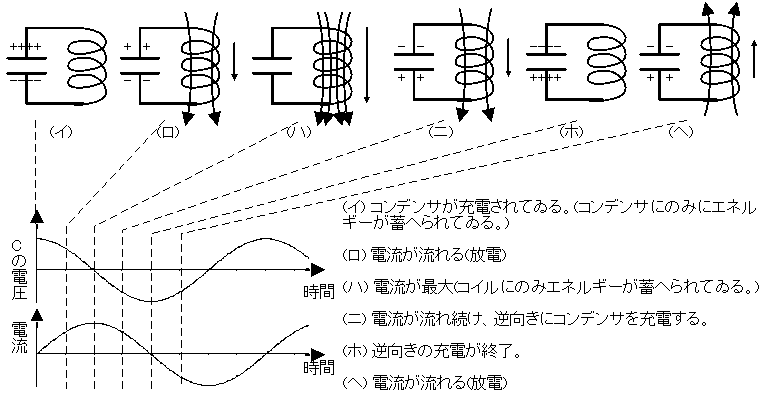
２－２－４　並列共振回路の動作

　損失がない理想的な並列共振回路は、共振周波数のタイミングでエネルギーをコンデンサとコイルの間で交互に受け渡し、エネルギーが保存される。しかし現実には損失があるので振動は次第に小さくなる。
　このやうに並列共振回路はエネルギーを蓄へるため「タンク回路」とも呼ばれる。

２－３　コンデンサの周波数特性

２－３－１　リアクタンスの周波数特性

　コンデンサのリアクタンスの式ではリアクタンスが周波数に反比例し減少する。周波数が大きくなるに従ひリアクタンスは限りなく0に近づく。これは理想的なコンデンサの話である。

(TDK株式会社の部品特性解析ソフト「SEAT」により出力した図に追記)

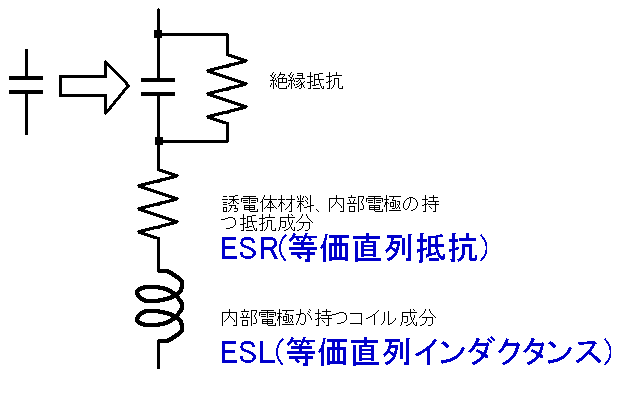
２－３－２　現実の周波数特性

　現実の部品は単調にリアクタンスが減少せずある周波数を境に上昇する。その理由は直列に寄生するコイル(インダクタンス、L)成分があるために直列共振現象を起こすためである。
　つまり現実のコンデンサは直列にコイルがつながつた直列共振回路となつてゐる。そのためコンデンサは直列共振周波数より低い周波数帯域で使ふ必要がある。さうでなければコンデンサとして機能せずコイルとして機能する。

２－４　コンデンサの使ひ方と反共振現象

２－４－１　組み合はせ

　広い周波数帯域の雑音をコンデンサでバイパスさせるには静電容量の異なる複数のコンデンサを並列に配置することになる。つまり静電容量の大きなコンデンサの自己共振周波数を超えた帯域で低いインピーダンスを与へる静電容量の小さいコンデンサを配置する。

　
　
(TDK株式会社の部品特性解析ソフト「SEAT」により出力した図)

　その際複数のコンデンサによつて得られるインピーダンス特性は、コンデンサ単体とは大きく異なつたものになる可能性がある。

２－４－２　反共振

　コンデンサは自己共振周波数以上でコイルの性質を示す、一方で並列にある小さな静電容量のコンデンサはそれより高い周波数までコンデンサの性質のままである。すると大きな静電容量のコンデンサの自己共振周波数から、小さな静電容量のコンデンサの自己共振周波数までの帯域では、大きなコンデンサと小さなコンデンサで並列共振回路が形成されることになる。この並列共振現象のことを反共振といふ。
　下の図は二つのコンデンサの単体インピーダンス特性を重ねたものである。二つのコンデンサの自己共振周波数の間で並列共振回路が構成される。

(TDK株式会社の部品特性解析ソフト「SEAT」により出力した図に追記)

　反共振周波数では下図のやうにインピーダンスが急激に高まることがある。そのため反共振周波数付近の雑音はバイパスされないことになる。

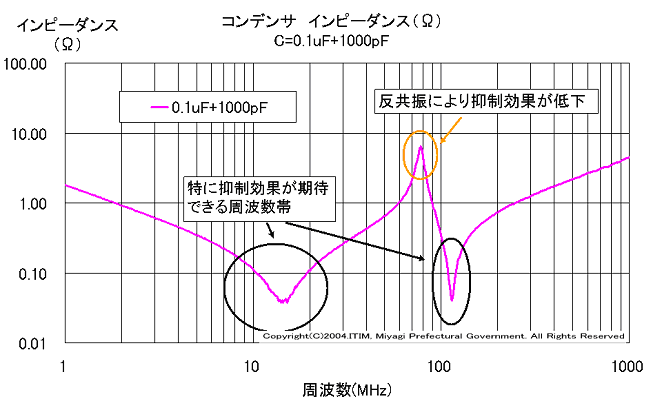
　宮城県産業技術総合センター「実装基板上での高周波電流阻止効果」より

文献

• 岡小天　他「高等学校物理」啓林館、昭和59年度用、第4章、第5章
• TDK(株)「コンデンサ・ワールド」第4回
• 宮城県産業技術総合センター「実装基板上での高周波電流阻止効果」