３－１ 交流信号の波長
３－２　伝送線路 (transmission line)
３－３　配線と静電場

３－１ 交流信号の波長

３－１－１　電磁波の速度

　電磁波(電波、光)の伝はる速さは真空中で秒速約300,000,000 (m)=300,000 (km)= 300M (m)。これを真空中の光の速さ(光速)といひ、物理学ではc(小文字)の記号で表してゐる。
　　　　　　　　c = 2.99792458 * 10^8 (m/s)

　電気信号は電線に沿つて伝はる電磁波のことである。
　電線を伝つて流れる電気信号は真空中よりも遅くなる。単線では0.98倍程度になる。ここでは議論を簡単にするために電気信号の伝はる速さを 300M (m/s)とする。

３－１－２　交流信号の周波数

　交流信号の周波数とは1秒間に1周期を何回繰り返すかであつた。
　50Hzの商用電源では1秒間に正弦波の1周期を50回繰り返す。

図 1　50Hz交流の時間変化(1秒間)

３－１－３　波長

　この50Hzの交流が長い電線を伝つて流れるとする。1秒後には300M(m)先に到達する。
　このとき電源から300M(m)先までそれぞれの地点の電圧を調べると、正弦波が50周期繰り返されてゐることがわかる。ここで正弦波1周期分の距離を波長といふ。波長はλ(ラムダ)の記号で表す。
　このことから電磁波の波長λと周波数fの関係は光速をcとして、
　　λ = c / f 　式3-1

の関係があることがわかる。

　改めて空間を進む波を考へる。ある時点から1周期の時間 (T) が経つと波の先端は、波の速度 (v) ×1周期の時間 (T) の距離に進むことになる。1周期分の距離を波長 (λ)といふので
　　λ = v T

の関係がある。

　今度は1秒後を考へる。0秒時点の波の先端は1秒後には v (m) 先の位置に進んでゐる。その間に f 回の周期が存在するので
　　v = f λ

の関係が存在する。

　ここで波の速さを真空中の電磁波の速さ c とすれば式3-1が得られる。

　50Hz交流の波長は
　　300M (m/s) / 50 (Hz) = 6M (m) = 6000 (km)
になる。地球の半径(約6700km)並に長い距離である。

３－１－４　位相差

　50Hz交流の話を続ける。電源から1500km離れた場所の電圧を考へてみる。ある時刻に電源では電圧が0であつたとする。このとき1,500km離れた地点はλ/4、90度位相がずれてゐるから、交流のピーク電圧が観測されることになる。このやうな場合は電源の場所との位相差を考慮せざるを得ない。


　一方1mしか離れてゐない場所は同じとみなして良い。位相差は
　　360° 1 (m) / 6M (m) = 60μ° = 0.00006°

となり電源と同じと言つて差し支へない。6000kmに対する1mは微々たるものだ。

３－１－５　波長が短い場合

　では周波数が高くなつて100MHzの交流について考へてみる。
波長は、
　　300M (m/s) / 100M (Hz) = 3 (m)

　1m離れた場所の位相差は
　　360° 1 (m) / 3 (m) = 120°

100MHzでは1m離れた場所の位相差が大きいので、50Hz交流の1,500km離れた地点と同様に扱はざるを得ない。

３－１－６　波長がもつと短い場合

　今度は1GHzの交流について考へてみる。
波長は、
　　300M (m/s) / 1G (Hz) = 0.3 (m) = 30 (cm)

　7.5cmでλ／４であり、少しの距離で大きな位相差に相当する。配線の距離がますます問題になる。

３－２　伝送線路 (transmission line)

　電気機器が実用化された頃、信号は電線を通じて瞬時に伝はると考へられてゐた。また電線の特性は抵抗分を考慮すれば充分と考へられてゐた。回路図の配線と同様の考へ方である。

　しかし現実には、信号は時間を掛けて遅れて伝はり、波が伝はることと同じであることがわかつた。波の伝播(でんぱ)の議論に基づいた電線、配線のことを「伝送線路」といふ。
　電線、配線の長さが取り扱ふ信号の波長に比べて無視できない大きさになると、伝送線路として取り扱はなくてはならない。一般に線路長が波長の1/10から1/100以下と短い場合は伝送線路として扱はず、単に接続用導線とみなして差し支へない場合が多い。

３－２－１　分布定数回路

　伝送線路を回路で表現すると、線路の長さ方向に沿つて微小なインダクタンス L、キャパシタンス C、抵抗 R、漏れコンダクタンス Gが無限個数分布してゐるモデルが考へられる。このモデルで表されるものを分布定数回路といふ。
これが直列に多数接続されてゐると考へる。

通常 R 、G は小さく損失は少ない。
これに対して、分布定数回路として考へる必要がないものを集中定数回路といふ。

３－２－２　媒質、波の反射

　波の伝播において、波が伝はる物質を媒質といふ。
　まづ光の伝播を考へてみる。光の伝播において重要なのは媒質の屈折率である。下図のやうに屈折率の異なるガラスが二つ張り合はされてゐるとする。光を一方のガラスから当てると光の一部はガラスの境界で反射される。屈折率が一致してゐない限り反射が起こる。

図 6 光の屈折と反射
　他にも光は真空中から異なる屈折率の媒質に入ると速度が低下する。その速さは媒質の屈折率により決る。
　電気信号の媒質は伝送線路である。そこで光の屈折率に類似する性質は「特性インピーダンス」である。更に伝送線路では電磁波の速さは伝送線路の絶縁物の誘電率により低下する。

３－２－３　伝送線路の種類

• 同軸ケーブル (coaxial cable)

(右の図はAgilent Technologies AppCADによる)
　同軸ケーブルは50Ωと75Ωの特性インピーダンスが規格として決つてゐる。特性インピーダンスは内部導体と外部導体の直径の比で決り、太さは様々なものがある。太いケーブルは伝送損失が小さい。代表的な波長短縮率は約67％。絶縁物の材質により波長短縮率は異なる。
　因みにこの構造を持つケーブルのことを「シールド線」といひ、そのうちインピーダンスを管理してゐるものを「同軸ケーブル」といひ、インピーダンスを管理してゐないシールド線を単に「シールド線」と呼ぶ。

• マイクロストリップライン（microstrip line）

マイクロストリップラインは、裏面に導体箔を形成した板状誘電体基板の表面に線状の導体箔を形成した構造を持つ伝送線路。
　表面導体から裏面導体に向かう方向の電界と、表面導体周囲を囲む方向の磁界によつて電磁波を伝送する。

(図はAgilent Technologies AppCADによる)

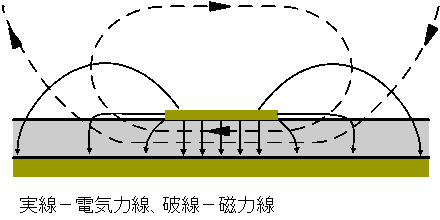
　表面導体の外側、空気中にはみ出してゐる電気力線が存在する。そのためマイクロストリップラインの近傍に金属を近付けると線路の動作に影響を与へる。

• ストリップライン(Stripline)

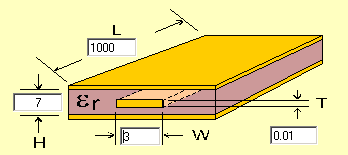
(図はAgilent Technologies AppCADによる)
　ストリップラインは、表裏面に導体箔を形成した板状誘電体基板の内部に線状の導体箔を形成した構造を持つ伝送線路。
　内部導体から外部導体に向かう方向の電界と、内部導体周囲を囲む方向の磁界によつて電磁波を伝送する。同軸ケーブルの外部導体の両側面を切り開いて2枚の板とし、内部導体を箔状に引き延ばした形状に相当する。
　伝送路から漏洩する電磁波が少ないという利点を有する反面、表面、裏面および内部の3層に導体箔パターンを形成する必要があり製造工程が複雑になる。
　携帯電話等の小型無線機器では、高密度実装のために6層基板や8層基板が使われるのが一般的であるためストリップラインを形成するに当り支障が無く、またストリップラインの真上や真下にも部品が配置できるためストリップラインが多用される。

• 平行二線式フィーダ

　昔テレビのアンテナ線として使はれてゐたリボンフィーダー(300Ω)やメガネフィーダー(200Ω)が代表例。テレビの給電線としては同軸ケーブルが主流となり、平行線フィーダーは用ゐられなくなつた。

　二つの線は電磁気的に結合してゐる。線の間隔を短くすると特性インピーダンスが低下する。このケーブルに金属を近付けるとケーブルの電磁気が乱され特性が変化する。

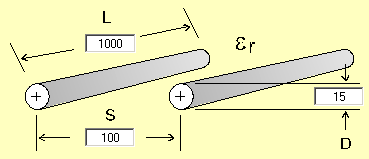
(図はAgilent Technologies AppCADによる)

下は Physics Software の Electric Field による図

• ツイストペア線 (撚り対線)

　ツイストペアケーブル（Twisted pair cable、ツイステッドペアケーブル）は、撚り対線（よりついせん）ともいひ、平行二線を撚り合はせたケーブルである。単なる平行線よりノイズを出しにくくかつ受けにくい。古くからある技術であるが、近年ではLANの配線に使はれる例がよく知られる。

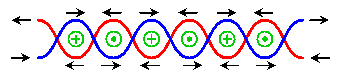
　上の図は撚り対線に流れる電流により発生する磁場を示すものである。隣接する区画の磁場の向きは反転してゐる。直流電流により発生する磁場の右ネジの法則により、各区画内側では図の向きに磁場が発生する。

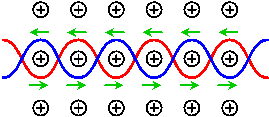
　上の図は撚り対線に対して一様に、変化する磁場を掛けて発生する電流を示すものである。各区間では同じ向きに逆起電力が発生するが、捻つて接続されてゐるので全体として電流は打ち消される。

３－２－４　伝送線路中の電磁波の速度

　伝送線路を構成する導体の間にある物質の誘電率により伝播する電磁波の速度Vpが決る。物質がなく真空の場合、電磁波の速度は光速である。Vpは位相速度とも呼ばれる。(Phase Velocityの略)

　ここに
　　Vp = 位相速度 (m/s)
　　c = 真空中の光速 (m/s) = 2.99792458e8 (m/s)
　　μs = 媒質の比透磁率(真空と比べた透磁率の比)
　　εs = 媒質の比誘電率(真空と比べた誘電率の比)
　電磁波の速度が遅くなると、伝送線路内の波長は短くなる。この短くなる比率を波長短縮率といふ。良くある同軸ケーブルの波長短縮率は約67％である。FR-4のガラスエポキシ基板で構成したマイクロストリップラインの波長短縮率は55%であり、真空中の約半分になる。
　波長短縮率は光速と伝送線路中の位相速度の比と同じことである。

３－２－５　伝送線路の特性インピーダンス

　同軸ケーブルを買ふときに、50Ωの同軸ケーブルなどといふがこの50Ωはどこの値なのか。ケーブルに50Ωの抵抗は付いてゐない。
　ケーブルの端と端で芯線の抵抗(A-A')、シールドの抵抗(B-B')を測つても50Ωより遥かに小さい抵抗が見えるだけである。また芯線とシールド線の間の抵抗(A-B)を測つても無限大の抵抗が見えるであらう。接続されてゐないのだから当然である。50Ωの値は発見できない。

　伝送線路の「特性インピーダンス」とはなにか。これはケーブルの終端に特性インピーダンスと同じ値の抵抗を接続すると、ケーブル上のどこで切つてもA-B間のインピーダンス(電圧と電流の比)が特性インピーダンスの値になるといふ性質を表してゐる。特性インピーダンスは の記号で表される。特性インピーダンスは「波動インピーダンス」「特性サージインピーダンス」とも呼ばれる。
　特性インピーダンスが50Ωの伝送線路は、ケーブルの先が50Ωのつもりで作つてあるケーブルと言へる。ケーブルの中では、信号に50Ωの状況が見えるやうになつてゐて、ケーブルの端に信号が到達するまで、50Ωの負荷を仮定して信号は進む。ケーブルの先に50Ωでない抵抗がつながつてゐる時はそこで反射が発生する。これは光の反射・屈折で屈折率の異なる物質に光が進んだときと同様のことである。ここで反射されなかつた信号は抵抗で消費される。
　反射が発生するとケーブルの中では見かけ上インピーダンスが変化して見え、50Ω均一にならない。

３－３　配線と静電場

　配線の(特性)インピーダンスが低いと外乱を受けにくくなり安定だといはれる。特性インピーダンスが低いのはその配線の静電容量が大きいからであり、静電容量が大きいのはその配線に接近して金属、グラウンドが存在するからである。その様子を静電場の分布から見る。

３－３－１　周囲に金属がない配線

　下は直線電流の等電位線を示した図である。配線はある電位を持つてゐて、無限の彼方(無限遠)が0Vであると仮定して配線から無限遠までの電位分布を表した図である。地図の等高線と同じ見方になる。等電位線が密になつてゐる部分は電場が大きい。等電位線が密になつてゐるところは電位の傾斜が大きく、それを電場が大きいといふ。

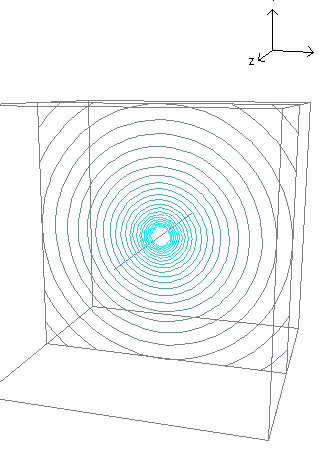
以下は http://www.falstad.com/mathphysics.html の 3-D Electrostatic Fields Applet による図。

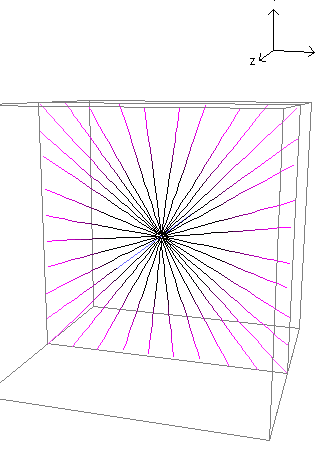
　次の図は電気力線を示す。電気力線は輻射状つまり四方八方均等に広がつてゐる。電気力線は正電荷から負電荷または無限遠までをつなぐ線で、この線が密集してゐる部分は電場が大きい。
　このやうな状態は、静電容量は小さいが配線から離れた場所であつても金属を近付けると静電容量が変化し易い。つまり周囲の影響を受け易い。

３－３－２　同一平面にグラウンドがある配線

　同一平面にグラウンドがある場合、配線とベタグラウンドの間に一次元的(線状)にコンデンサが形成される。この間に電場が集中し、それ以外の方向への電場は弱くなる。従つて周囲に全く金属がない状態よりも周囲の影響を受けにくい。静電容量も大きくなり、特性インピーダンスも小さくなる。

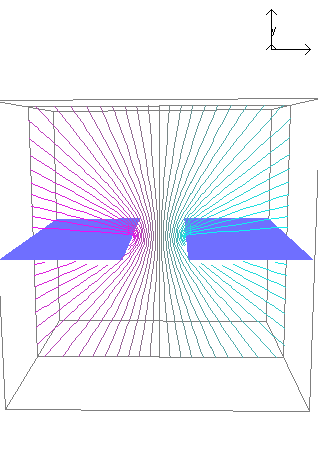
３－３－３　裏面にグラウンドがある配線

　これはマイクロストリップラインそのものになる。この場合、裏面のグラウンドと面状にコンデンサが形成され、その間に電場が集中する。それ以外への電場は弱くなる。よつて周囲の影響は受けにくくなる。

文献

• 岡小天　他「高等学校物理」啓林館、昭和59年度用、第3章
• 武部幹「回路の応答」コロナ社、昭和56年4月、6　分布定数回路の応答、p.118
• Wikipedia「反射」「伝送線路」の項
• 中島将光「マイクロ波工学」森北出版
• 後藤尚久「電波がわかる本」オーム社、H15年11月、第2章
• 伊藤健一「分布定数回路のはなし」日刊工業、2003年11月